Mathematische Kunstausstellung, Teil 9 – Funktionen als Abbildungen

In der Mathematik werden Funktionen auch „Abbildungen“ genannt: Jeder Ausgangswert entspricht einem Punkt, der auf einen anderen Punkt (den Funktionswert) abgebildet wird. Alle Ausgangswerte zusammen bilden das Urbild, alle Funktionswerte zusammen das Abbild.
Was liegt also näher, als die Funktionen komplexer Zahlen als ebensolche „Abbildungen“ eines wirklichen Bildes darzustellen?

Nehmen wir als „Versuchskaninchen“ dieses Meerschweinchen, und passen wir es in ein Koordinatensystem ein, damit wir nicht nur die „Abbildung“ dieses Bildes, sondern der ganzen Zahlenebene mitverfolgen können:

Die einfachsten Abbildungen sind die Translation (Verschiebung), die Drehung, und die Streckung (Vergrösserung). Eine Verschiebung kommt mathematisch so zustande, dass zu jedem Punkt des Urbildes derselbe Wert addiert wird. Dann verschiebt sich das ganze Bild um diese Distanz. Eine Streckung entspricht einer Multiplikation: Werden z.B. die Koordinaten jedes Punktes mit 3 multipliziert, dann wird das Bild dreifach vergrössert. Bei einer Drehung wird der Winkel jedes Punktes (bezüglich des Nullpunktes) verändert. Ich glaube, es ist nicht nötig, diese einfachen Abbildungen bildlich darzustellen.

Was geschieht aber, wenn wir jeden Punkt des Urbildes mit einer komplexen Zahl multiplizieren? Unten z.B. die Funktion y = x · (1 + 0.4i). Wir sehen, dass das Ergebnis eine „Drehstreckung“ ist: Das Bild wird gedreht und gleichzeitig leicht vergrössert.

Ein weiteres Beispiel dieser Art: y = x · (1 + 1.4i) :

Versuchen wir jetzt etwas anderes und erheben wir unser Meerschweinchen ins Quadrat (y = x²). Das gibt bereits eine nicht mehr so ganz einfache Abbildung:

Und wenn wir einen gebrochenen Exponenten gebrauchen, sagen wir y = x^1.6 ? – Das gibt eine ähnliche Abbildung, nur scheint es hier, sie sei auf halbem Wege stehengeblieben:

Nehmen wir schliesslich noch den Kehrwert (y = 1/x). Das gibt eine ganz interessante Abbildung, bei welcher der Nullpunkt in unendliche Ferne rückt und der „unendlich ferne Punkt“ auf den Nullpunkt abgebildet wird. Die Koordinatenlinien werden dabei zu Kreisen, die alle durch den Nullpunkt gehen; und unser armes Meerschweinchen strebt mit seinem Hinterteil gegen die Unendlichkeit!

Geordnetes Punktemischen

Nun noch eine Abbildung, die nichts mit den komplexen Zahlen zu tun hat. (Oder vielleicht doch? In der Mathematik gibt es so viele überraschende Zusammenhänge, dass man sich nicht wundern sollte, wenn letztendlich fast alles mit allem irgendwie zusammenhängt …)

Nehmen wir wieder unser Meerschweinchen, das uns bereits so gute Dienste geleistet hat. Das digitalisierte Bild besteht aus lauter quadratischen Bildpunkten. Der Computer speichert diese nicht als zweidimensionales Bild, sondern als eine lange Kette von Daten hintereinander. Nach dem letzten Punkt der obersten Reihe kommt einfach der erste Punkt der nächsten Reihe, und so weiter. Der Computer braucht dann nur noch die zusätzliche Information, wie lang eine Reihe ist, um das Bild richtig darstellen zu können.

Lassen wir nun den Computer diese „Datenkette“ mischen, und zwar auf folgende Weise: Die Position jedes Punktes wird mit einer konstanten Zahl multipliziert, sagen wir 97. Wir verschieben also Punkt 1 auf Platz 97, Punkt 2 auf Platz 194, Punkt 3 auf Platz 291, und so weiter. Natürlich werden wir damit irgendwann einmal über das Ende des ursprünglichen Bildes hinausschiessen. Wenn das passieren sollte, dann springen wir einfach wieder zum Anfang des Bildes und zählen von da weiter. Mathematisch gesprochen, kommt jeder Punkt a auf den Platz „97a modulo die Gesamtzahl aller Bildpunkte“. (Offenbar hat diese Abbildung also mit der modularen Arithmetik zu tun, die wir in Teil 2 und Teil 3 behandelten.)
Mathematiker werden schnell herausfinden, dass die Sache einen kleinen Haken hat: Wenn mein konstanter Multiplikator zufällig einen gemeinsamen Teiler hat mit der Gesamtzahl der Bildpunkte, dann werden in der Abbildung einige Punkte doppelt belegt, während andere gar nicht vorkommen. Deshalb wählen wir als Multiplikator am besten eine Primzahl (und eine, die nicht gerade ein Faktor der Bildweite oder -höhe ist).

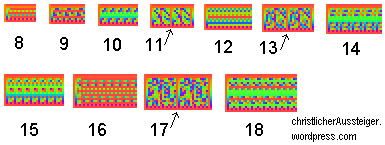
Auf das Ergebnis dieser Abbildung wenden wir nun wiederum dieselbe Abbildung an, und so weiter. Hier sehen wir die ersten sechs Schritte dieser Transformation:

Man könnte annehmen, dass das Bild bei fortgesetzter Transformation immer chaotischer wird. Dem ist aber nicht so (weshalb ich diese Transformation „geordnetes Mischen“ nenne). Im Gegenteil, an gewissen Stellen erscheinen immer wieder verkleinerte, etwas verzerrte Abbilder des ursprünglichen Bildes. Nach einer ganz bestimmten Anzahl von Schritten ginge sogar wieder unser ursprüngliches Meerschweinchen heil und unversehrt aus dieser Prozedur hervor! (Man kann mathematisch beweisen, dass genau dann, wenn Punkt 1 wieder auf Punkt 1 abgebildet wird, auch alle übrigen Punkte wieder an ihrem ursprünglichen Platz sind. Es sind dazu also maximal so viele Schritte nötig, wie das Bild Punkte enthält. Das sind bei unserem Bild genau 19398.)

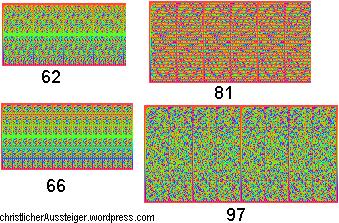
Manchmal braucht man aber viel weniger Schritte, um wieder das ursprüngliche Bild zu erhalten. Hier z.B. eine solche „Mischung“, die bereits im siebten Schritt zur Ausgangsstellung zurückkehrt. (Der Multiplikator ist hier 6, und die Gesamtzahl der Bildpunkte ist 6⁶-1):

Hier noch einige weitere Bilder, die beim „Mischen“ des Meerschweinchens entstanden sind:

(Schritt 8)	(Schritt 13)
(Schritt 30)	(Schritt 52)
(Schritt 65)	(Schritt 79)
(Schritt 91)	(Schritt 98)

Fanden Sie diesen Artikel interessant? Dann interessiert Sie sicher auch dieses Buch zum Mathematiklernen durch eigenes Forschen und Entdecken. Weitere Informationen hier.

Mathematische Kunstausstellung (Teil 3): Modulare Potenzen-Perserteppiche

Modulare Potenzen-Perserteppiche

In der vorhergehenden Folge haben wir die Zahlen der Multiplikationstabelle verschieden eingefärbt, je nach dem Rest (Modulo), den sie beim Teilen durch eine bestimmte Zahl ergeben. Dann machten wir etwas Ähnliches mit den Quadrat- und Kubikzahlen, und bewunderten die dadurch entstehenden Kunstwerke.

Wir können aber modulare Potenzfunktionen auch so darstellen, dass wir nicht den Exponenten, sondern den Teiler als Konstante wählen. Wir zeichnen also die Funktion z = y^x mod n für verschiedene Zahlen n. Wir haben fast dasselbe schon mit der Multiplikationstabelle gemacht: dort zeichneten wir die Funktion z = xy mod n. Wir sahen dabei, dass sich jeweils ein Muster von n x n Feldern wiederholte. Wie sehen diese Wiederholungen bei der Potenzfunktion aus?

In „y-Richtung“ (wenn y die Basis der Potenz ist) gibt es logischerweise eine Wiederholung, sobald y = n ist, denn dann potenziert sich der Rest von y, der hier wieder Null ist (und dann wieder 1, 2, 3, usw). Ich habe deshalb die Bilder jeweils auf der Höhe von n abgeschnitten. In „x-Richtung“ gibt es offensichtlich auch eine Wiederholung; aber es ist nicht so einfach vorauszusagen, wo genau diese eintritt!

Dies sind die Bilder für alle n von 8 bis 18:

Wir sehen, dass hier jede Zahl ihre besondere Eigenart hat.
– Wenn n eine Potenz von 2 ist (z.B. 8 oder 16), wird das Bild vorwiegend rot (= Rest Null). Logisch: Jede gerade Zahl, wenn man sie genügend oft potenziert, ergibt ein Vielfaches von 8 bzw. 16, und von da an ist der Rest immer Null.
– Wenn n eine Primzahl ist, dann erscheint jeweils an einer bestimmten Stelle ein charakteristischer senkrechter roter Strich, nach welchem sich das Muster wiederholt. (In den Bildern mit einem Pfeil bezeichnet.) Dies widerspiegelt den „Kleinen Satz von Fermat“, wonach a^n-1 – 1 für alle a von 1 bis n-1 durch n teilbar ist, wenn (und nur wenn) n eine Primzahl ist. Der rote Strich befindet sich also genau an der Stelle n-1, und es handelt sich hier um den Rot-Ton, der einem Rest von 1 entspricht.
– Für andere n ergeben sich immer wieder andere charakteristische, teppichähnliche Muster, die sich nach einer bestimmten (meist kürzeren) Periode wiederholen.

Hier einige weitere Beispiele mit zusammengesetzten Zahlen:

Auf dem nächsten Bild sehen wir links zwei Zahlen (62 und 66), die beim Teilen durch 4 den Rest 2 ergeben. Die Bilder aller dieser Zahlen enthalten in der Mitte einen breiten waagerechten grünen Streifen. (Siehe auch oben die Zahlen 10, 14 und 18.) Der Leser möge selber errechnen, woher das kommt.
– Die Zahl 81 ist die vierte Potenz von 3, weshalb jedes durch 3 teilbare y spätestens von der vierten Potenz an einen waagerechten roten Strich ergibt.
– 97 ist nochmals ein Beispiel für eine Primzahl.

Und hier noch einige Beispiele von etwas grösseren Zahlen:

(216: Eine Zahl mit vielen Teilern.)

(247 ist keine Primzahl! 13 x 19 = 247. Deshalb liegen die senkrechten roten Striche nicht bei 247-1=246, und bei genauer Betrachtung stellt man auch fest, dass sie nicht durchgehend sind.)

(256 = 2⁸)

(257 ist hingegen wieder eine Primzahl.)

In der nächsten Folge, so Gott will, werden wir einen anderen Bereich der Mathematik auf die darin verborgenen Kunstwerke untersuchen.

Fanden Sie diesen Artikel interessant? Dann interessiert Sie sicher auch dieses Buch zum Mathematiklernen durch eigenes Forschen und Entdecken. Weitere Informationen hier.

Mathematische Kunstausstellung (Teil 2): Modulare Arithmetik

In der ersten Folge dieser Serie haben wir uns vorwiegend mit der Multiplikationstabelle beschäftigt – ein Thema, das schon Kindern in den ersten Schuljahren zugänglich ist und ihnen zeigt, dass man mit Mathematik „Kunstwerke“ produzieren kann. Ich habe auch kurz meine Beweggründe dafür ausgeführt, eine solche „mathematische Kunstausstellung“ zu veranstalten.

Modulare Arithmetik im Einmaleins

In der ersten Folge haben wir die Zahlen der Multiplikationstabelle auf verschiedene Arten eingefärbt: nach ihren Endziffern, und nach ihrer Grösse (Zahlwert). Wir können sie auch nach anderen Kriterien einfärben, z.B. gerade/ungerade. Dann erhalten wir folgendes Muster:

0	0	0	0	0	0	0	0	0	0	0
0	1	2	3	4	5	6	7	8	9	10
0	2	4	6	8	10	12	14	16	18	20
0	3	6	9	12	15	18	21	24	27	30
0	4	8	12	16	20	24	28	32	36	40
0	5	10	15	20	25	30	35	40	45	50
0	6	12	18	24	30	36	42	48	54	60
0	7	14	21	28	35	42	49	56	63	70
0	8	16	24	32	40	48	56	64	72	80
0	9	18	27	36	45	54	63	72	81	90
0	10	20	30	40	50	60	70	80	90	100

Auf den ersten Blick sehen wir, dass es in dieser Tabelle viel mehr gerade als ungerade Zahlen gibt. Das liegt natürlich daran, dass eine gerade Zahl, multipliziert mit irgendeiner Zahl, immer eine gerade Zahl ergibt. (Hier liegt auch die Antwort auf die Frage in der ersten Folge, warum es so wenige Einmaleinszahlen gibt, die auf 1, 3, 7 oder 9 enden.)

Abgesehen vom Spiel mit den Farben, können solche Tabellen auch helfen, Fehler zu vermeiden. Wenn der Schüler die Tabelle selber schreibt und das Farbmuster irgendwo „gestört“ ist, dann ist die Zahl dort wahrscheinlich falsch. Wenn das Gesetz von Gerade und Ungerade einmal erkannt ist, dann wird der Schüler auch nicht mehr behaupten, 7 x 8 sei 65. Er erkennt dann nämlich sofort, dass das Ergebnis nicht ungerade sein kann, wenn die Multiplikation eine gerade Zahl (8) enthält.

– Das Kriterium „gerade/ungerade“ kann auch so umschrieben werden: Welcher Rest ergibt sich, wenn wir die Zahl durch 2 teilen? – Dann können wir natürlich statt 2 irgendeine andere Zahl wählen. In der untenstehenden Tabelle erhält jede Zahl ihre Farbe je nachdem, ob sie beim Teilen durch 3 den Rest 0, 1 oder 2 ergibt:

0	0	0	0	0	0	0	0	0	0	0
0	1	2	3	4	5	6	7	8	9	10
0	2	4	6	8	10	12	14	16	18	20
0	3	6	9	12	15	18	21	24	27	30
0	4	8	12	16	20	24	28	32	36	40
0	5	10	15	20	25	30	35	40	45	50
0	6	12	18	24	30	36	42	48	54	60
0	7	14	21	28	35	42	49	56	63	70
0	8	16	24	32	40	48	56	64	72	80
0	9	18	27	36	45	54	63	72	81	90
0	10	20	30	40	50	60	70	80	90	100

Und hier teilen wir jetzt durch 4:

0	0	0	0	0	0	0	0	0	0	0
0	1	2	3	4	5	6	7	8	9	10
0	2	4	6	8	10	12	14	16	18	20
0	3	6	9	12	15	18	21	24	27	30
0	4	8	12	16	20	24	28	32	36	40
0	5	10	15	20	25	30	35	40	45	50
0	6	12	18	24	30	36	42	48	54	60
0	7	14	21	28	35	42	49	56	63	70
0	8	16	24	32	40	48	56	64	72	80
0	9	18	27	36	45	54	63	72	81	90
0	10	20	30	40	50	60	70	80	90	100

Offensichtlich wiederholt sich hier immer dasselbe Muster von 4 x 4 Feldern. Ausserdem hat dieses Muster jeweils in der Mitte ein Feld mit derselben Farbe wie der „Rand“, nämlich Rest 0 (warum wohl?).

In der nächsten Tabelle malen wir die Zahlen gemäss ihrem Fünferrest an. Ist es eine Überraschung, dass sich hier ein Muster von 5 x 5 Feldern wiederholt?

0	0	0	0	0	0	0	0	0	0	0
0	1	2	3	4	5	6	7	8	9	10
0	2	4	6	8	10	12	14	16	18	20
0	3	6	9	12	15	18	21	24	27	30
0	4	8	12	16	20	24	28	32	36	40
0	5	10	15	20	25	30	35	40	45	50
0	6	12	18	24	30	36	42	48	54	60
0	7	14	21	28	35	42	49	56	63	70
0	8	16	24	32	40	48	56	64	72	80
0	9	18	27	36	45	54	63	72	81	90
0	10	20	30	40	50	60	70	80	90	100

Noch ein (fast) letztes Beispiel dieser Art: der Rest beim Teilen durch 6. Man kann hier auch darüber nachdenken, in welcher Weise sich die Muster unterscheiden, wenn die Teilungszahl einerseits eine Primzahl, bzw. andererseits eine zusammengesetzte Zahl ist.

0	0	0	0	0	0	0	0	0	0	0
0	1	2	3	4	5	6	7	8	9	10
0	2	4	6	8	10	12	14	16	18	20
0	3	6	9	12	15	18	21	24	27	30
0	4	8	12	16	20	24	28	32	36	40
0	5	10	15	20	25	30	35	40	45	50
0	6	12	18	24	30	36	42	48	54	60
0	7	14	21	28	35	42	49	56	63	70
0	8	16	24	32	40	48	56	64	72	80
0	9	18	27	36	45	54	63	72	81	90
0	10	20	30	40	50	60	70	80	90	100

Würden wir statt des Sechserrests den Zehnerrest wählen, dann erhielten wir eine Kombination aller „Endziffern-Bilder“ aus der ersten Folge.

Hier bewegen wir uns im Gebiet der modularen Arithmetik, ein interessanter Bereich der Zahlentheorie. Kurz gesagt geht es darum, dass man statt mit den kompletten Zahlen zu rechnen, lediglich mit dem Rest (=Modulo) rechnet, den die Zahlen beim Teilen durch eine bestimmte konstante Zahl ergeben. Dieser Rest macht nämlich die Rechenoperationen genau gleich mit wie die kompletten Zahlen. Eine bekannte Anwendung davon ist die „Neunerprobe“: Man kann eine Rechnung auf ihre Richtigkeit überprüfen, indem vergleicht, ob die Operation auch stimmt, wenn man die Neunerreste der einzelnen Glieder und des Ergebnisses nimmt.

Diese Modulo-Funktion bringt aber auch interessante Kunstwerke hervor. Hier z.B. die Multiplikationstabelle modulo 256, mit dem Nullpunkt in der Bildmitte. Es erscheinen bemerkenswerte sich überlagernde Muster:

Etwas mehr modulare Arithmetik

Das folgende Bild stellt die einfache Funktion z = x mod y dar, wobei z der Farbton ist. (D.h. die Farbe stellt den Rest dar, den x geteilt durch y ergibt.) Die „Regenbogenskala“ wird jeweils gleichmässig über den ganzen Bereich der möglichen Reste verteilt:

Was passiert, wenn wir statt einfach den Rest der Zahl x zu nehmen, die Zahl zuerst quadrieren? – Hier die Funktion z = x² mod y:

Wir treiben das Spiel noch ein wenig weiter und stellen z = x³ mod y graphisch dar:

Man könnte annehmen, dass bei höheren Potenzen weitere interessante Muster erscheinen. Das aber nicht unbedingt so. Hier ein aufs Geratewohl ausgewähltes Beispiel, das auf den ersten Blick sehr ungeordnet aussieht, obwohl es zweifellos seine Gesetzmässigkeiten hat: z = x¹⁰⁵ mod y:

In einer kommenden Folge werden wir dieses Thema noch ein wenig ausweiten.

Fanden Sie diesen Artikel interessant? Dann interessiert Sie sicher auch dieses Buch zum Mathematiklernen durch eigenes Forschen und Entdecken. Weitere Informationen hier.